
Nathan Otey of ThinkerAnalytix continues his run-down on how to use argument maps to evaluate the quality of an argument.
Last time, I explained how argument maps work, including the basic components that are common to all arguments: a main claim, and three types of premises (co-premises, sub-premises, and independent premises) which can be combined in different structures to visualize any argument.
Today, I want to show you how to use an argument map to determine whether an argument is any good. A map is extremely useful for evaluating an argument because it gives you a precise, systematic, step-by-step process to walk through.
I ended last time by asking you to consider this argument map, whose main claim is that schools should return to meeting in-person in the fall:
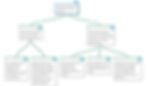
This argument is certainly relevant to our moment, but is it any good? Should we be persuaded to accept the main claim? I’ll show you how I approach evaluating the quality of an argument represented in a map, and let you carry on evaluating the rest of the argument yourself.
To analyze the quality of an argument map, I usually start at the bottom and work my way up, moving from left-to-right. I start my analysis by considering each premise and asking: Is this premise true? If the premise is false, then I can simply ignore it and move on to the next premise. If the premise is true, I then ask: How relevant is this premise to proving the claim above it? (Or, to put it differently, how strong is the inference from this premise to the claim above.) If the premise is true and the inference is strong, then that small section of the argument is good. But if the premise is false or the inference is weak, then we should not be persuaded to accept the claim under consideration.
To illustrate, let’s start with premise 3.4 on the bottom-left of our argument over opening schools. Is this statement true? My answer would be: generally, yes. I don’t have any data to back this up, but I would be very surprised if most school-age children can focus on their schoolwork by sitting at a screen by themselves for more than 3 or 4 hours per day. And even if most students were capable of doing so, it might not be fair to ask them to do so on a daily basis. I like to indicate that I think a premise is true by making its background blue in the argument map, as in:

Once I’ve decided that the premise is true (or at least reasonable) I then ask: how strong is the inference from 3.1 to 2.1? Does 3.1 give a persuasive reason to believe that 2.1 is true? In this case, I think this inference is fairly weak. We can indicate that an inference is weak by making the inference line thinner in the argument map:

Why do I think this inference is weak, even though the premise is true? It is based on my experience as a teacher and student that tells me most students do not actually pay attention for more than 3 or 4 hours of an in-person school day. Just because students are sitting in a chair in a classroom for 6 or 7 hours per day, does not ensure that they are actually engaging with the content, as anyone who has worked in a school can tell you. Thus, even if students are spending less time overall each day on school-related activities because they’re working remotely, they may still spend at least as much time engaged in learning. So, the truth of 3.1 does not persuade me to accept 2.1.
In a previous discussion of Toulmin Maps, Jonathan talked about the role of objections in an argument diagram. I’m going to use an argument mapping version of objections to add a “so-what?” objection (the one with the red bar above it) that gives me a reason to believe the inference between premise 3.1 and premise 2.1 above it is pretty weak:

Now, in order to decide whether to believe 2.1, I still need to evaluate the other premise supporting it, which is now numbered 3.3.
Is premise 3.3 true? I think it is mostly false. I like to indicate that I have evaluated a premise as false by giving it an orange background:

Why do I think that 3.3 is mostly false? In other words, why do I think that teachers can still be just as effective when working remotely? Two reasons. First, teachers will probably be more effective when they don’t have to spend time and energy commuting to a school building every day and can focus instead on simply being effective at their jobs. Second, it will be easier for teachers to manage their classrooms in a remote environment. Oftentimes, a physical classroom dynamic can be challenging due to disruptive or distracted students who can detract from teachers’ ability to focus on pedagogy and content. But in the digital environment is generally easier to manage what is going on since teachers can control functions like chat, small group breakouts, screen-sharing, etc.
I’ve represented my beliefs (which you are free to disagree with/rebut) with two “Not so!” objections to 3.3 in my argument map, demonstrating why I think premise 3.3. is false:

Since I’ve decided that 3.3 isn’t true, I don’t need to evaluate the strength of the inference from 3.3 to 2.1 since 3.3 can’t be a persuasive reason if it’s not true!
So far, I have determined that premise is not well supported, which means it can only do so much to support the main claim of the argument.
However, in order to decide whether this argument is good overall, I still need to evaluate the other branch of the argument map, the one that talks about how remote learning might disproportionately impact students who are already disadvantaged, an analysis I will leave for you to do based on what you have just learned.
Like the translation of real-world arguments into argument maps, argument analysis takes some time to master but will eventually become second nature. And to show you how powerful these techniques can be, next time I’d like to present a full-blown logic-checker that evaluates an editorial about a controversial real-world topic: defunding the police.